Trigonometry

Right triangle

TODO

Trigonometry functions

Sine

The sine of an angle always has a value between $-1$ and $1$, and it’s a periodic function that repeats its value every $2\pi$ radians (or $360°$).

In the right triangle

In the right triangle, the sine measures the relation between the opposite side and the hypotenuse.

To calculate the sine of an angle in a right triangle, use the following equation:

$$\sin \theta =\frac{\text{opposite side}}{\text{hypotenuse}}$$

Considering the following image:

The sine of the angle $\theta$ is defined by:

$$\sin \theta =\frac{a}{b}$$

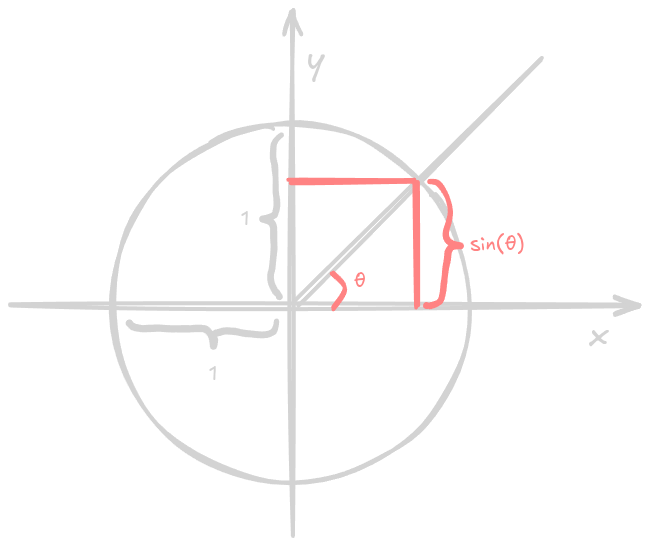
In the unit circle

In the unit circle, the sine represents the height (ordinate) of the corresponding point of a specific angle. See the image below:

Cosine

The cosine of an angle always has a value between $-1$ and $1$, and it’s a periodic function that repeats its value every $2\pi$ radians (or $360°$).

In the right triangle

In the right triangle, the cosine measures the relation between the adjacent side and the hypotenuse.

To calculate the sine of an angle in a right triangle, use the following equation:

$$\cos \theta =\frac{\text{adjacent side}}{\text{hypotenuse}}$$

Considering the following image:

The cosine of the angle $\theta$ is defined by:

$$\cos \theta =\frac{a}{b}$$

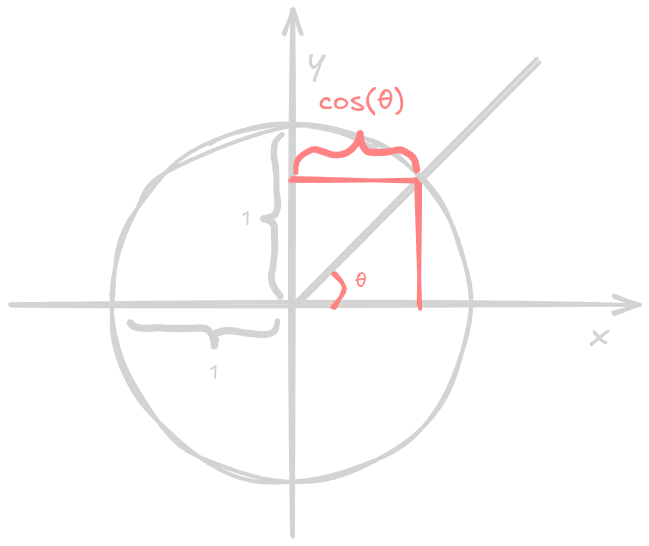
In the unit circle

In the unit circle, the cosine represents the width (abscissa) of the corresponding point of a specific angle. See the image below:

Tangent

In the right triangle

In the right triangle the tangent represents the relation between its sides. To calculate the tangent use the following formula:

$$\tan \theta =\frac{\text{opposite side}}{\text{adjacent side}}$$

Consider the following image:

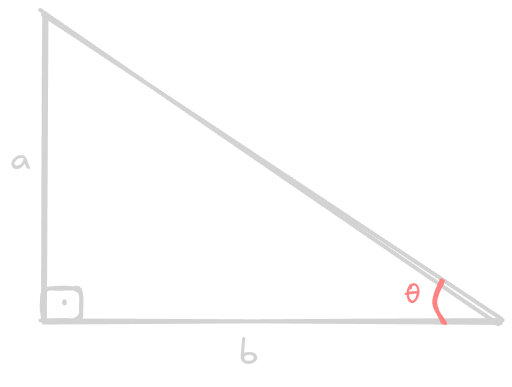
The tangent of the angle $\theta$ is defined by:

$$\tan \theta =\frac{a}{b}$$

One important thing to note is that, when the angle $\theta$ corresponds to the angle formed between the hypotenuse and the x-axis, the tangent of $\theta$ is the slope of the hypotenuse:

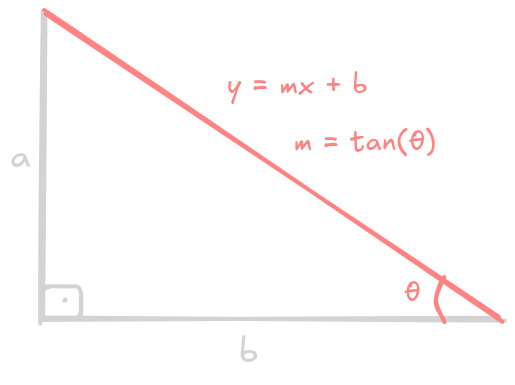
In the image above, $m$, which represents the slope of the hypotenuse, is equal to $\tan \theta$.

In the unit circle

In the unit circle, the tangent represents the relation between sine and cosine of an angle. Here’s the tangent equation:

$$\tan \theta =\frac{\sin \theta }{\cos \theta }$$

The image below gives a visual representation of the tangent of an angle:

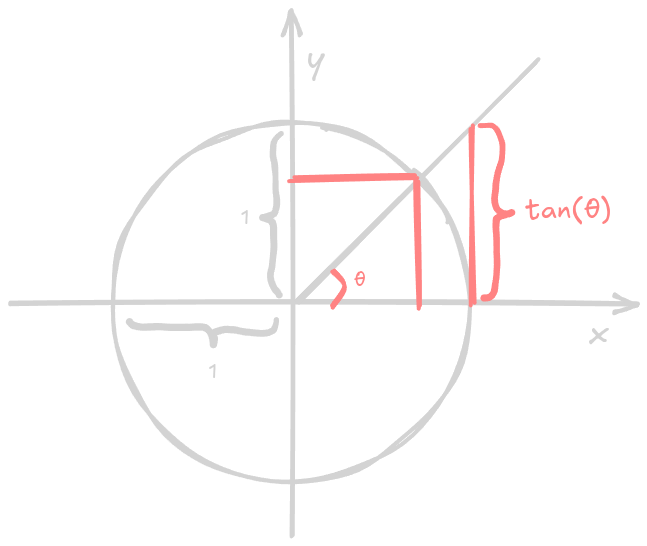
Cotangent

In the right triangle

In the right triangle, cotangent is the inverse of the tangent. It is the relation between the sides, just like tangent, but inverted:

$$\cot \theta =\frac{\text{adjacent side}}{\text{opposite side}}=\frac{1}{\tan \theta }$$

In the unit circle

The image below gives a visual representation of the cotangent of an angle:

Secant

In the right triangle

In the right triangle, the secant is the inverse of the cosine. It also represents the relation between the hypotenuse and the adjacent side, but inverted:

$$\sec \theta =\frac{\text{hypotenuse}}{\text{adjacent side}}=\frac{1}{\cos \theta }$$

In the unit circle

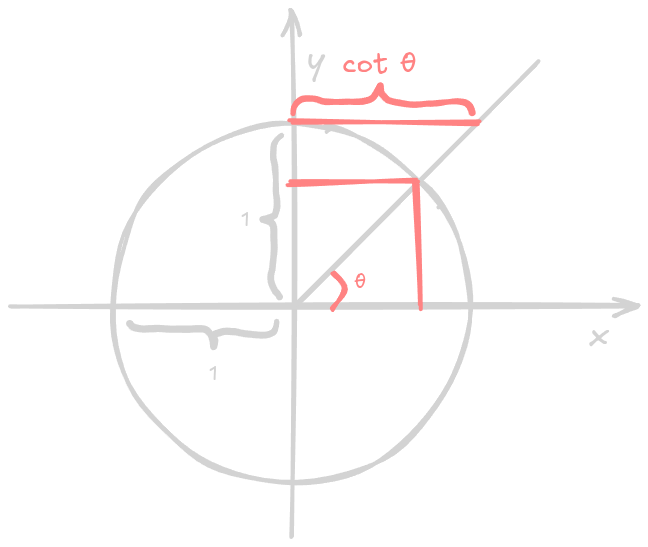
In the unit circle, the secant has the following visual representation:

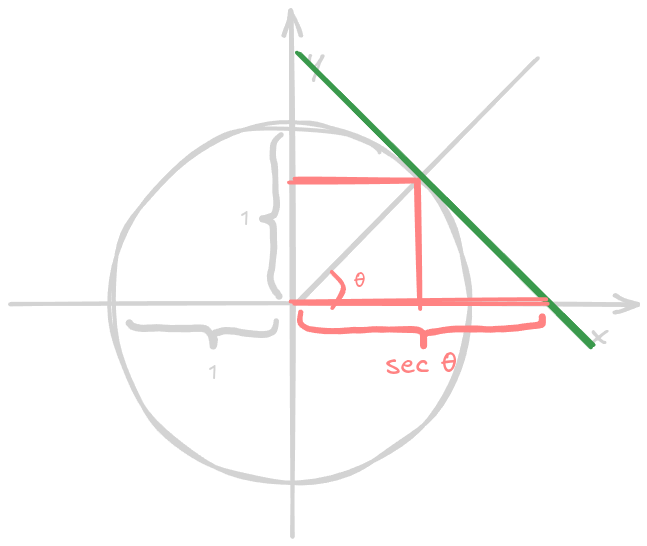
Cosecant

In the right triangle

In the right triangle, the cosecant is the inverse of the sine. It also represents the relation between the hypotenuse and the opposite side, but inverted:

$$\sec \theta =\frac{\text{hypotenuse}}{\text{opposite side}}=\frac{1}{\sin \theta }$$

In the unit circle

In the unit circle, the cosecant has the following visual representation:

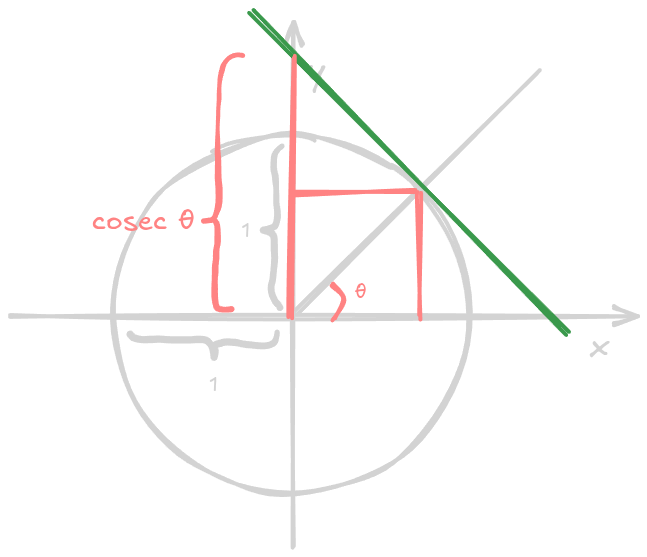
Notable angles

Notable angles are some specific angles that have well known sine and cosine values and are easy to memorize.

The angles and its values are listed in the table below:

angle	$30°=\frac{\pi }{6}$	$45°=\frac{\pi }{4}$	$60°=\frac{\pi }{3}$
$\sin$	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$
$\cos$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$

Trigonometry Identities

Pythagorean

$$(\sin \theta {)}^2+(\cos \theta {)}^2=1$$

because

$$\frac{{\text{opposite side}}^2}{{\text{hypotenuse}}^2}+\frac{{\text{adjacent side}}^2}{{\text{hypotenuse}}^2}$$ $$\frac{{\text{opposite side}}^2+{\text{adjacent side}}^2}{{\text{hypotenuse}}^2}$$ $$\frac{{\text{hypotenuse}}^2}{{\text{hypotenuse}}^2}=1$$

Cos(a + b)

$$\cos (\theta +\alpha )=\cos \theta \cdot \cos \alpha -\sin \theta \cdot \sin \alpha$$

Sin(a + b)

$$\sin (\theta +\alpha )=\sin \theta \cdot \cos \alpha +\cos \theta \cdot \sin \alpha$$

Tan(a + b)

$$\tan (\theta +\alpha )=\frac{\tan \theta +\tan \alpha }{1-\tan \theta \cdot \tan \alpha }$$

TODO

---

Radians to degrees:

$$\frac{\pi }{2}=90°$$

The sum of two angles that are not the right angle in a right triangle must result in $90°$ So the value of a third angle is the difference between $90°$ and the other angle

$$\sin (\frac{\pi }{2}-\alpha )=\cos \alpha$$ $$\cos (\frac{\pi }{2}-\alpha )=\sin \alpha$$